I. Why mesoscopic?

The mesoscopic description of physical systems bridges the gap between the microscopic and macroscopic descriptions. The former (microscopic) approach acounts for all constituents that make up the system and their fundamental interactions. At the mesoscopic level, the individual constituents are collectivelly described by means of a distribution function, defined over phase space. The macroscopic description is oblivious of the phase-space structure and instead relies on a further coarse-graining, replacing the distribution function by a finite set of macroscopic observables, such as energy density, fluid velocity, etc.
In principle, each level of description is accurate on its respective scale. Highly non-equilibrium or nano-scale processes may represent the applicability limit of the macroscopic description, while fundamentally quantum systems, which are formed of a sufficiently small number of constituents, may prove challenging for mesoscopic models.
In recent years, several arenas which bring together all three levels of description have arised in a variety of systems. For example, multiscale phenomena are ubiquitous challenges in astrophysics or cosmology, such as the supernova explosions or large scale structure formation. Below, the focus of the discussion will be on microscale systems, such as the quark-gluon plasma formed in relativistic heavy ion colliders, which also require a multiscale treatment.

II. Helical vortical effects

In the microscopic world, present day heavy ion colliders are able to create the quark-gluon plasma (QGP), which exhibits properties which are remarkably indicative of a nearly-perfect fluid behaviour. The macroscopic description of the collective behaviour of the QGP relies on the correct realisation of the transport laws that govern its evolution, which are derived from the more fundamental mesoscopic description.
The vorticity of the QGP formed in non-central collisions can induce a net polarisation, which was measured by the STAR collaboration at the Relativistic Heavy Ion Collider (RHIC) at the Brookhaven National Laboratory (BNL). This polarisation can be considered to be a signature of anomalous transport, which traces its roots to the anomalous violation of classical conservation laws via quantum fluctuations. When driven by local vorticity, these laws are referred to as vortical effects.

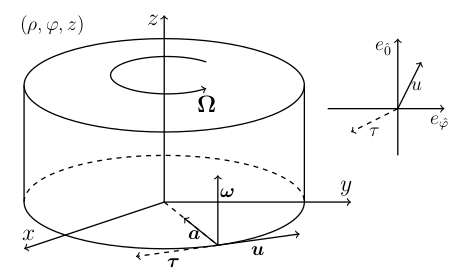
Fig. 1: Kinematic tetrad corresponding to rigid rotation, comprised of the four-velocity \(u = \Gamma(\partial_t + \Omega \partial_\varphi)\), acceleration \(a = -\rho \Gamma^2 \partial_\rho\), vorticity \(\omega = \Omega \Gamma^2 \partial_z\) and circular vector \(\tau = -\Omega^3 \Gamma^5 (\rho^2 \Omega \partial_t + \partial_\varphi)\) (Figure reproduced from Ref. [2]).

The vortical effects can be revealed by considering a quantum state of Dirac fermions at finite temperature \(T\) undergoing rigid rotation with angular velocity \(\Omega\). In this case, it is convenient to employ the kinematic tetrad comprised of the four-velocity \(u^\alpha\), acceleration \(a^\alpha\), vorticity \(\omega^\alpha\) and circular vector \(\tau^\alpha\), depicted in Fig. 1 above. The Lorentz factor \(\Gamma\) corresponding to rigid rotation with angular velocity \(\Omega\) is \[ \Gamma = \frac{1}{\sqrt{1 - \rho^2 \Omega^2}}. \] It can be seen that \(\Gamma\) diverges as the speed of light surface (SLS) is approached, when \(\rho \Omega \rightarrow 1\).

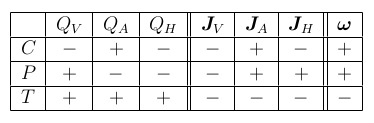
Table 1: Parity (\(+\) for even and \(-\) for odd) of the vector (\(V\)), axial (\(A\)) and helical (\(H\)) charge densities and (spatial) charge currents, as well as of the kinematic vorticity \(\mathbf{\omega}\), under the C, P and T transformations (Table reproduced from Ref. [1]).

In Refs. [1,2], novel transport laws (dubbed helical vortical effects) were uncovered by taking into account polarisation imbalance via the helicity chemical potential \(\mu_H\). This novel thermodynamic variable forms a triad together with the electrical (vector) and chiral (axial) chemical potentials, \(\mu_V\) and \(\mu_A\). These chemical potentials are dual to the corresponding charge densities \(Q_\ell\ (\ell\in\{V,A,H\})\), which are constructed using the (classically) conserved charge currents \(J_l^\alpha\) (the axial charge current is classically conserved only when the fermions are massless). The properties of the helicity charge current, as well as of its corresponding chemical potential, under the charge conjugation (\(C\)), spatial inversion or parity (\(P\)) and temporal inversion (\(T\)) transformations, are summarised in Table 1.
QFT calculations reveal that the charge currents obey the following constitutive relations: \[ J_\ell^\alpha = Q_\ell u^\alpha + \sigma^\tau_\ell \tau^\alpha + \sigma^\omega_\ell \omega^\alpha. \] The first term, \(Q_\ell u^\alpha\), corresponds to the usual charge flow along the fluid macroscopic velocity. At large temperatures, the charge densities are given up to \(O(T^{-1})\) by: \[ Q_V = \frac{\mu_V T^2}{3} + \frac{4T \mu_A \mu_H}{\pi^2} \ln 2 + \frac{\mu_V(\mu_V^2 + 3\mu_A^2 + 3\mu_H^3)}{3\pi^2}, \] \[ Q_A = \frac{\mu_A T^2}{3} + \frac{4T \mu_H \mu_V}{\pi^2} \ln 2 + \frac{\mu_A(\mu_A^2 + 3\mu_H^2 + 3\mu_V^3)}{3\pi^2}, \] \[ Q_H = \frac{\mu_H T^2}{3} + \frac{4T \mu_V \mu_A}{\pi^2} \ln 2 + \frac{\mu_H(\mu_H^2 + 3\mu_V^2 + 3\mu_A^3)}{3\pi^2}, \] where the local temperature and chemical potentials are given in terms of their values on the rotation axis (denoted using the subscript \(0\)) and of the Lorentz factor \(\Gamma\): \[ T = \Gamma T_0, \qquad \mu_\ell = \Gamma \mu_{\ell,0}. \] The second term, \(\sigma^\tau_\ell \tau^\alpha\), represents a circular counterflow (provided \(\sigma^\tau_\ell Q_\ell > 0\)) along the circular vector \(\tau^\alpha\). Up to \(O(T^{-1})\), the circular conductivity \(\sigma^\tau_\ell\) is given by: \[ \sigma^\tau_V = \frac{\mu_V}{6\pi^2}, \qquad \sigma^\tau_A = \frac{\mu_A}{6\pi^2}, \qquad \sigma^\tau_H = \frac{\mu_H}{6\pi^2}. \] The term \(\sigma^\omega_\ell \omega^\alpha\) gives rise to current flow along the local vorticity \(\omega^\alpha\). While \(u^\alpha\) and \(\tau^\alpha\) vanish on the rotation axis, \(\omega^\alpha\) persists here, allowing the vortical effects to manifest themselves whenever a non-vanishing vorticity is present. The vortical conductivities are given up to \(O(T^{-1})\) terms by \[ \sigma^\omega_V = \frac{2\mu_H T}{\pi^2} \ln 2 + \frac{\mu_V \mu_A}{\pi^2}, \qquad \sigma^\omega_A = \frac{T^2}{6} + \frac{\mu_V^2 + \mu_A^2 + \mu_H^2}{\pi^2}, \qquad \sigma^\omega_H = \frac{2\mu_V T}{\pi^2} \ln 2 + \frac{\mu_H \mu_A}{\pi^2}. \] The robustness of the above transport laws at finite mass (and vanishing axial chemical potential) is discussed in Ref. [2], bearing in mind that when the mass is non-vanishing, the axial chemical potential can no longer be consistently introduced in the theory. In general, the massless expressions remain valid for \(M \lesssim T\). This can be seen in Fig. 2, where the charge density \(Q_\pm = Q_V \pm Q_H\) and the circular conductivity \(\sigma^\tau_\pm = \sigma^\tau_V \pm \sigma^\tau_H\) are represented with respect to the particle mass, \(M\).

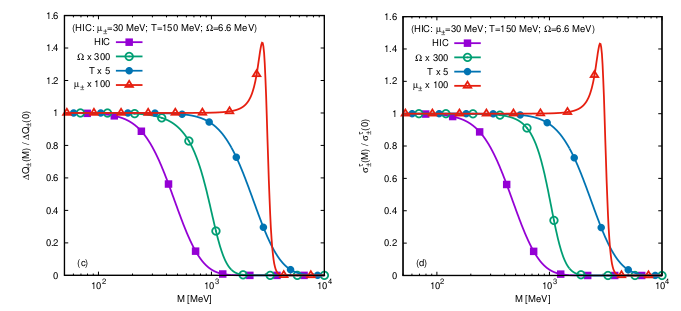
Fig. 2: Ratio between the massive and massless values of the charge density \(Q_\pm = Q_V \pm Q_H\) (left) and circular conductivity \(\sigma^\tau_\pm = \sigma^\tau_V \pm \sigma^\tau_H\), represented with respect to the mass \(M\), given in MeV (Figures reproduced from Ref. [2]).

In all of the above expressions, terms which are divergent as the SLS is approached are present. This issue is addressed more fully in Ref. [3] for the case of vanishing helical and axial chemical potentials. Fig. 3 below shows the typical radial profile of the energy density for fermions of mass \(M\), obtained both within the QFT (\(E_\beta\)) and relativistic kinetic theory \(E_F\) frameworks. Comparing the results obtained within these two approaches, it can be seen that quantum corrections become dominant close to the speed of light surface (SLS).

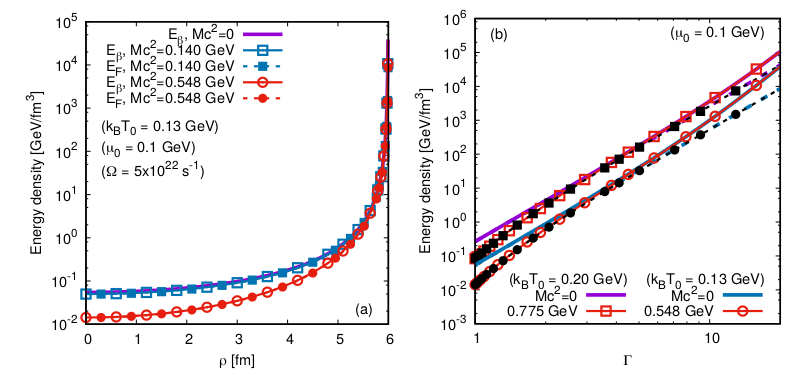
Fig. 3: Dependence on (a) the distance \(\rho\) from the rotation axis, measured in fm, and (b) on \(\Gamma\), of the energy densities obtained within the quantum (\(E_\beta\), empty symbols and continuous lines) and relativistic kinetic theory (\(E_F\), filled symbols and dashed lines) frameworks. The results are shown for various values of the fermion particle mass \(M\). It can be seen that the quantum corrections become dominant close to the SLS (Figures reproduced from Ref. [3]).

[1] V. E. Ambruș, M. N. Chernodub, Helical vortical effects, helical waves, and anomalies of Dirac fermions, arXiv:1912.11034 [hep-th].
[2] V. E. Ambruș, Helical massive fermions under rotation, JHEP08(2020)016.
[3] V. E. Ambruș, E. Winstanley, Exact solutions in quantum field theory under rotation, Book chapter in Strongly Interacting Matter Under Rotation. Edited by F. Becattini, J. Liao and M. Lisa Lecture Notes in Physics, vol. 987 (Springer, Cham, 2021).

III. Phase diagram of helically imbalanced QCD matter

Strongly interacting matter consists of quarks and gluons, which are regarded in the theory of quantum chromodynamics (QCD) as elementary particles interacting due to the colour charge. According to the standard model of particles, a quark can have one of six flavours and are arranged in pairs of charge \(+2/3\) and \(-1/3\), distributed over three generations. The lightest generation consists of the up (\(u\), charge \(+2/3\), mass \(\sim 2\) MeV) and down (\(d\), charge \(-1/3\), mass \(\sim 5\) MeV) quarks. The second generation, consists of the charm (\(c, 2/3, 1275\) MeV) and strange (\(s, -1/3, 95\) MeV) quarks. The third generation consists of the even heavier top (\(t, 2/3, 173\) GeV) and bottom (\(b, -1/3, 4.2\) GeV) quarks. The heavy quarks from the second and third generations are unstable and therefore much rarer (exotic) in normal conditions than the \(u\) and \(d\) quarks.
In usual conditions, the quarks are bound together in colourless states, called hadrons. Hadrons are typically mesons and baryons. The former consist of a quark-anti-quark pair, such as the \(\pi^0 (u {\bar u} + d {\bar d})\), \(\pi^+ (u {\bar d})\) and \(\pi^- (d {\bar u})\) mesons. The latter are formed of three quarks (baryons) or three antiquarks (anti-baryons), the most common baryons being the proton (\(uud\)) and neutron (\(udd\)). As either the temperature or the density (modelled via the vector chemical potential, \(\mu_V\)) are increased, the quarks are expected to break free from their hadronic prisons, giving rise to the quark-gluon plasma.
An effective approach to model the QCD phase transition is to consider that the quarks acquire a dynamical mass which is significantly heavier when the quarks are confined into hadrons than when they are free. One such approaches is the linear \(\sigma\) model with quarks, described using the following Lagrangian: \[ \mathcal{L}_{\rm LSM} = {\bar \psi} [i \gamma^\mu \partial_\mu - g(\sigma +i\gamma^{5} \vec{\tau} \cdot \vec{\pi})]\psi + \frac{1}{2} \left(\partial_\mu \sigma\partial^\mu \sigma + \partial_\mu \pi^0 \partial^{\mu}\pi^{0}\right) + \partial_\mu \pi^+ \partial^{\mu}\pi^{-} - V(\sigma,\vec{\pi}), \] where the potential \(V = \frac{\lambda}{4}(\sigma^2 + \vec{\pi}^2 - v^2)^2 - h\sigma\) achieves its minimum when \(\langle \vec{\pi}\rangle = 0\) and \(\langle \sigma\rangle = f_\pi\). The value of the free parameters appearing above are taken such that \(f_\pi = 93\) MeV is equal to the pion decay constant. In the mean field approximation, the pion and sigma fields are considered to be frozen at their classical expectation values, completely neglecting their quantum fluctuations. In this case, the term \(g \langle \sigma\rangle = M\) behaves like a dynamical quark mass, which is decided by the expectation value of the pseudoscalar field \(\sigma\). Choosing \(g = 3.3\), the quark mass in the vacuum is \(M = 307\) MeV, which is about one third of the mass of a nucleon, while the pion mass, given by \(m_\pi^2 = \lambda(\langle \sigma\rangle^2 - v^2)\), takes the value \(m_\pi = 138\) MeV when \(v = 87.7\) MeV and \(\lambda = 19.7\). The mass of the \(\sigma\) meson is \(m_\sigma = 600\) MeV.

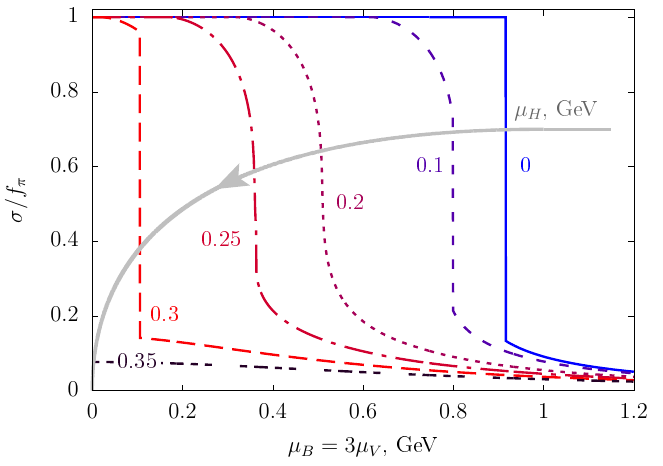
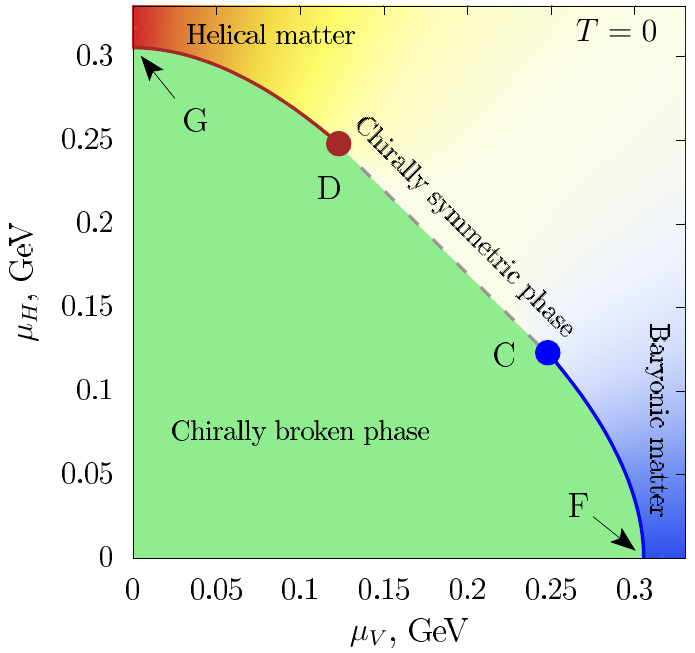
Fig. 4: (top) Expectation value of \(\langle \sigma \rangle\), normalised with respect to its vacuum value \(f_\pi\), at vanishing temperature, as a function of the baryon chemical potential \(\mu_B = 3\mu_V\), for various values of the helical chemical potential \(\mu_H\). (bottom) Phase diagram corresponding to the chiral phase transition at \(T = 0\) (Figures reproduced from Ref. [4]).

In the vacuum, the above paragraph describes how the quarks achieve a dynamical mass due to the \(\sigma\) field. At finite temperature, density (modelled using the vector chemical potential, \(\mu_V\)) and polarisation (modelled using the helicity chemical potential, \(\mu_H\)), the expectation value \(\langle \sigma \rangle\) can be regardede as a dynamic variable, which takes a value such that the free energy \(\Omega\) of the system is minimised. Since the full details of the calculation are presented in Ref. [4], here only the results are discussed. One can expect that \(\langle \sigma \rangle\) will decrease dramatically when the temperature or chemical potentials exceed a threshold value. This is shown for the case of vanishing temperature in the top panel of Fig. 4. It can be seen that, at small values of the vector and helical chemical potentials, \(\mu_V\) and \(\mu_H\), \(\sigma\) takes its vacuum expectation value, \(f_\pi\). For fixed values of \(\mu_H\), which are below the critical value of 305 MeV, \(\sigma\) drops rapidly when \(\mu_V\) exceeds a threshold value, which decreases as \(\mu_H\) is increased. The sharp drop is indicative of a first-order phase transition, while when the transition follows a smooth curve, the phase transition is of crossover type. This is better illustrated in the bottom panel of Fig. 4, where it can be seen that there exists a (previously unknown!) region of crossover phase transition at intermediate values of \(\mu_V\) and \(\mu_H\).

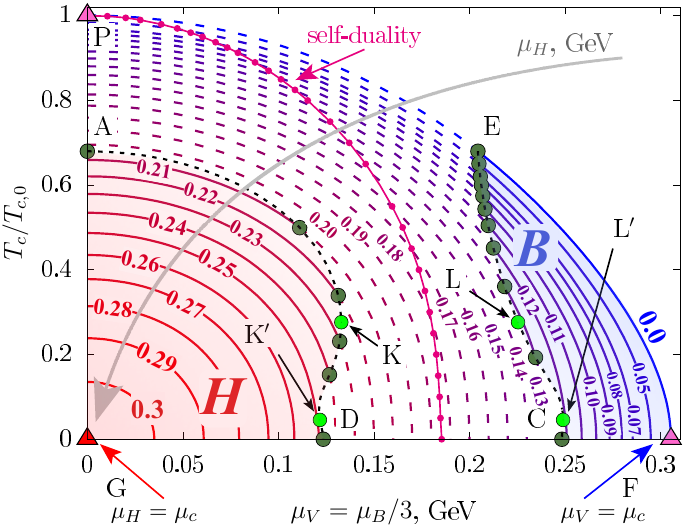
Fig. 5: Phase diagram of the chiral phase transition at various values of \(\mu_H\). The axes correspond to the temperature \(T\), normalised with respect to the critical value \(T_{c,0} \simeq 146.5\) MeV, and vector chemical potential \(\mu_V\). Each contour shown on the diagram corresponds to the phase transition line for a fixed value of the helical chemical potential \(\mu_H\). The solid part of these lines denote a first order phase transition, while the dotted parts correspond to crossover transitions. The magenta self-duality line indicates the contour where \(\mu_V = \mu_H\) (Figure reproduced from Ref. [4]).

Fig. 5 shows the phase diagram at finite temperature. The blue and red regions correspond to baryonic and helical matter and are labelled \(B\) and \(H\). The purple self-duality line corresponds to the contour on which \(\mu_V = \mu_H\). In all respects, the duality between \(\mu_V\) and \(\mu_H\) is preserved in this phase diagram. For example, the point \(F\) corresponds to the phase transition at vanishing \(\mu_H\) and \(T\), which occurs at the critical value \(\mu_V = 305\) MeV. The symmetric point \(G\) corresponds to vanishing \(\mu_V\) and \(T\) and indicates that the phase transition occurs when \(\mu_H = 305\) MeV. Thus, \(F\) and \(G\) are obtained from each other by performing the simultaneous exchange \(\mu_V \leftrightarrow \mu_H\).

[4] M. N. Chernodub, V. E. Ambruș, Phase diagram of helically imbalanced QCD matter, Phys. Rev. D 103 (2021) 094015.

IV. QFT on curved space

The Minkowski (flat-space) metric represents an idealisation in which the effect of matter on the space-time fabric is completely neglected. In reality, any distribution of mass-energy induces deviations from the flat-space limit. In particular, the gravitational attraction is entirely due to the space-time curvature.
Taking into account the interaction between a quantum field and the gravitational field can reveal interesting effects, of which probably the Hawking effect (predicting the evaporation of black holes through thermal emission of radiation) remains the most spectacular. Another important result refers to the so-called conformal anomaly (also known as Weyl anomaly), due to which the trace of the stress-energy momentum of a conformally-coupled massless fermion field aquires a non-vanishing value. Of the curved backgrounds which have seen the most interest in the context of QCD is the anti de Sitter (adS) space, due to the adS/CFT conjecture, which allows the study of a conformally invariant, strongly interacting QFT via a dual weakly-coupled gravitational system on the boundary of adS (one extra dimension compared to the original system is required). To study the effect of rotation in such systems, the results presented in this section focus on free fermions in rigid rotation on adS. Ref. [6] discusses the behaviour of the fermion condensate at finite \(T\) and \(\Omega\), but vanishing chemical potentials, as well as its surface and volume integrals. Ref. [5] focusses more generally on anomalous transport. The technique used for the analysis is point-splitting, starting from the vacuum Feynman two-point function, \(S^F_{\rm vac}(x,x')\). When the rotation parameter is sufficiently small and the SLS does not develop within the confinement of the adS boundary, the thermal two-point function \(S^F_{\beta_0,\Omega}(x,x')\) can be obtained as [5,6]: \[ S^F_{\beta_0,\Omega}(x,x') = \sum_{j = -\infty}^\infty (-1)^j e^{-j \beta_0 \Omega S^z} S_{\rm vac}^F(\tau +ij \beta_0, \varphi + i j \beta_0 \Omega; x'). \] The full details of the calculations can be found in Ref. [5]. It is remarkable that in the large temperature limit and for massless fermions, the constitutive equations obtained on the Minkowski space are exactly recovered. For example, the axial charge current is \(J^\mu_A = \sigma^\omega_A \omega^\mu\), where \(\omega^\mu\) is the local vorticity corresponding to rigid rotation, while the axial vortical conductivity is \[ \lim_{M\rightarrow 0} \sigma^\omega_{A} = -\frac{\omega^3 \cos^2\omega r}{2\pi^2 \Omega \Gamma^2} \sum_{j = 1}^\infty \frac{(-1)^j \sinh\frac{\omega j \beta_0}{2} \sinh\frac{\Omega j \beta_0}{2}} {(\sinh^2\frac{\omega j \beta_0}{2} - \omega^2 \overline{\rho}^2 \sinh^2\frac{\Omega j \beta_0}{2})^2} = \frac{T^2}{6} + O(T^{-1}). \] It is remarkable that the fermion condensate (FC) aquires a non-vanishing value, which persists even in the massless limit: \[ \lim_{M \rightarrow 0} FC = -\frac{\omega^3}{2\pi^2} \cos^4\omega r \sum_{j = 1}^\infty \frac{(-1)^j \cosh \frac{\omega j \beta_0}{2} \cosh \frac{\Omega j \beta_0}{2}} {(\sinh^2 \frac{\omega j \beta_0}{2} + \cos^2 \omega r - \omega^2 \overline{\rho}^2 \sinh^2\frac{\Omega j \beta_0}{2})^2} = \frac{\omega^3}{4\pi^2} + O(T^{-1}). \] It can be seen that, at large temperature, the FC attains a constant value. The volume and surface integrals of the FC, \(V_{\beta_0, \Omega}^{\rm FC}\) and \(S_{\beta_0, \Omega}^{\rm FC},\) can also be computed [6] and are shown in Fig. 6 below.

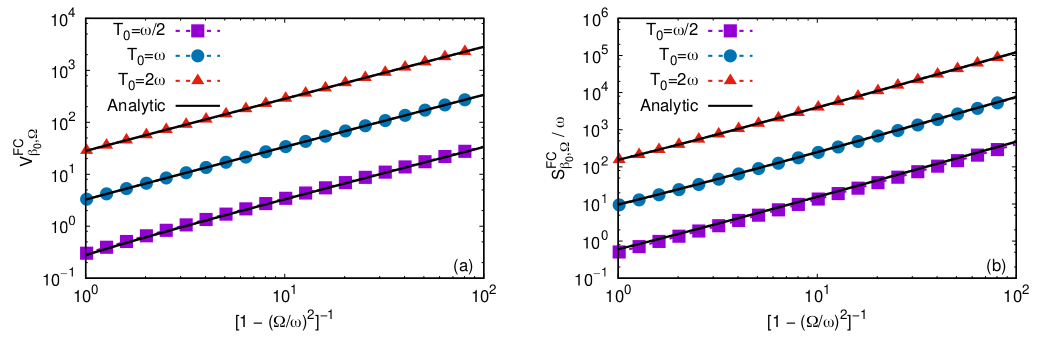
Fig. 6: Volume (a) and surface (b) integrals of the FC, represented with respect to \((1 - \Omega^2 / \omega^2)^{-1}\), where \(\Omega\) is the rotation parameter and \(\omega\) is the inverse adS radius of curvature (the Ricci scalar is \(R = -12 \omega^2\)). Figure reproduced from Ref. [6].

[5] V. E. Ambruș, E. Winstanley, Vortical effects for free fermions on anti-de Sitter space-time, arXiv:2107.06928 [hep-th].
[6] V. E. Ambruș, Fermion condensation under rotation on anti-de Sitter space, Acta Phys. Pol. B Proc. Suppl. 13 (2020) 199.

V. QFT between boundaries

Rigid rotation implies a linear increase of the azimuthal velocity with the distance \(\rho\) to the rotation axis. At angular velocity \(\Omega\), the speed of light surface (SLS), where the fluid velocity reaches the speed of light, is equal to \(\Omega^{-1}\) (for the value typical for heavy ion collisions, \(\Omega \simeq 10^{22}\,{\rm s}^{-1}\), the distance to the SLS is \(c \Omega^{-1} = 0.3\ {\rm fm}\)). Close to the SLS, the macroscopic quantities such as the energy density diverge. Surprisingly, quantum corrections become dominant due to a higher order divergence close to the SLS. This can be seen in Fig. 3 above. For these reasons, the study of rigidly rotating states can only be self-consistently performed when the system is bounded such that the SLS is excluded from the system. One example was the study of the anti-de Sitter space discussed in Sec. IV above, which incorporates a natural boundary. This section focuses on enclosing the usual Minkowski system inside a cylindrical boundary, placed at distance \(R\) from the rotation axis.
While in hydrodynamics, the boundary conditions (b.c.s) are readily understood as fixing the value (Dirichlet b.c.s) or the flux (Neumann b.c.s) of a given quantity, in QFT, the b.c.s are formulated in a more abstract way, usually at the level of the field operator itself. For the Klein-Gordon field, both the Dirichlet- and Neumann-type boundary conditions are captured within a more general scheme, known as Robin boundary conditions, which entail that the field \(\Phi\) obeys on a boundary of normal vector \(n_\mu\) the following equation: \[ (A + B n^\mu \nabla_\mu) \Phi(x) = 0.\] On the surface of the cylinder of radius \(R\), it is convenient to introduce the parameter \(\Psi = A R / B\), such that the Robin boundary condition becomes: \[ R \frac{\partial \Phi}{\partial R} + \Psi \Phi = 0, \] where the Dirichlet boundary conditions are recovered when \(\Psi \rightarrow \infty\), while the Neumann boundary conditions correspond to \(\Psi = 0\). A challenging task is to establish the connection between the value of \(\Psi\) and the properties of the quantum state in the vicinity of the boundary.
The quantum corrections (computed with respect to an equivalent classical, relativistic kinetic theory system) also manifest themselves as a departure from the perfect fluid form expected in global thermodynamic equilibrium. Examples include the anomalous transport highlighted in Sec. II. The relativistic equivalence between mass and energy make the concept of fluid four-velocity itself ambiguous. For the specific case of the rigidly rotating system, one natural choice for the four-velocity would be that corresponding to rigid rotation, \(u = \Gamma(\partial_t + \Omega \partial_\varphi)\). This choice establishes the so-called beta (or thermometer) frame. However, this definition seems somewhat artificial or external, since it relies on the a priori characterisation of the ensuing quantum state. A more intrinsic definition of the four-velocity leads to the so-called energy (or Landau) frame, when \(u_L^\mu\) is regarded as an eigenvector of the stress-energy tensor, \(T^\mu{}_\nu u_L^\nu = E_L u_L^\mu\), where the eigenvalue \(E_L\) is the Landau frame energy density. Solving this equation, we find that the azimuthal velocity \(v_L = \rho u^{\varphi} / u^t\) is related to the components of the stress-energy tensor via \[ \frac{v_L}{1 + v_L^2} = \frac{\rho T^{t\varphi}}{T^{tt} + \rho^2 T^{\varphi\varphi}}. \] Evaluated on the boundary, the above relation can be taken as the starting point for an interative procedure to find the value of \(\Psi\) that ensures a given velocity \(v_b = v_L(\rho = R)\) on the boundary (more details can be found in Ref. [7]). The left panel of Fig. 7 below shows how the value of \(v_b\) depends on the Robin parameter \(\Psi\). In the right panel of Fig. 7, the profiles of \(v_L\) are shown for selected values of \(\Psi\), ranging from Neumann (\(\Psi = 0\)) to Dirichlet (\(\Psi = \infty\)) boundary conditions.

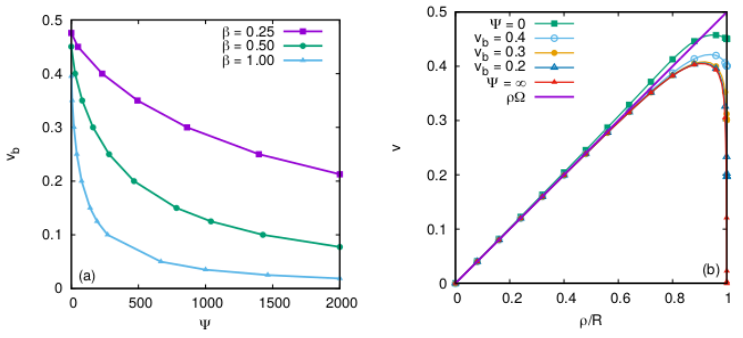
Fig. 7: (a) Landau velocity on the boundary \(v_b\) for various values of the inverse temperature \(\beta\) (expressed in units of \(R / \hbar c\)) as a function of the Robin parameter \(\Psi\). (b) Profiles of the Landau velocity for various values of \(\Psi\), at inverse temperature \(\beta = 0.5 R\). In both cases, the rotation paramter obeys \(R \Omega = 0.5 c\). Figures reproduced from Ref. [7].

[7] V. E. Ambruș, Rigidly-rotating quantum thermal states in bounded systems, arXiv:1904.01123 [hep-th]